Topic 5: Gaussian Mixture Model, EM (Expectation, Maximization)

GMM

The general GMM assumption

• \(P(Y)\): There are \(k\) components
• \(P(X|Y)\): Each component generates data from a multivariate Gaussian with mean \(\mu_i\) and covariance matrix \(\Sigma_i\)

Each data point is sampled from a generative process:

1. Choose component \(i\) with probability \(P(y=i)\)
2. Generate datapoint \(\sim N(\mu_i, \Sigma_i)\)


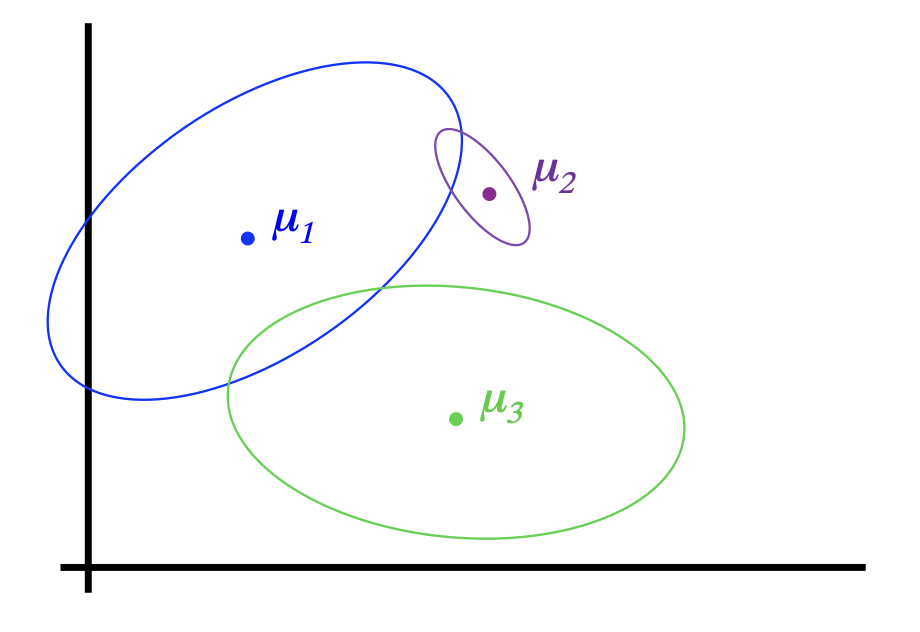
Gaussian Mixture Model (GMM)

What models should we use depends on \(X\). We can make fewer assumptions:

• What if the \(X_i\) co-vary?
• What if there are multiple peak?

Gaussian Mixture Models!

• \(P(Y)\) is multinomial
• \(P(X|Y)\) is a multivariate Gaussoan distribution

\[ P(X = x_j | Y = i) = \frac{1}{(2\pi)^{m/2} \|\Sigma_i\|^{1/2}} \exp\left(-\frac{1}{2} (x_j - \mu_i)^T \Sigma_i^{-1} (x_j - \mu_i)\right) \]

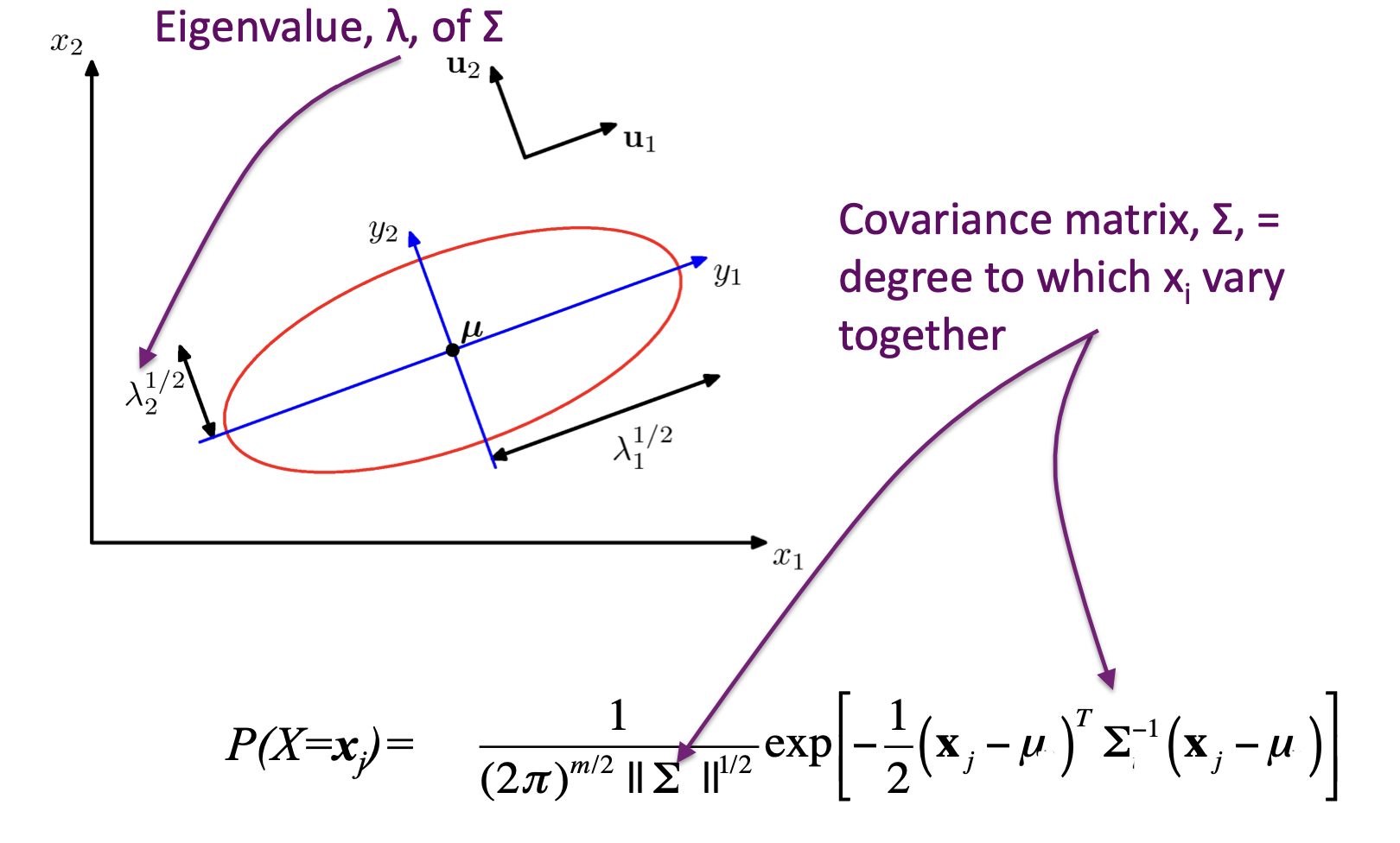
Multivariate Gaussian

\[ P(X = x_j) = \frac{1}{(2\pi)^{m/2} \|\Sigma\|^{1/2}} \exp\left(-\frac{1}{2} (x_j - \mu)^T \Sigma^{-1} (x_j - \mu)\right) \]


\[ \Sigma \propto \text{identity matrix} \]


\[ \Sigma = \text{diagonal matrix} \]

\[ X_i \text{ are independent ala Gaussian NB} \]


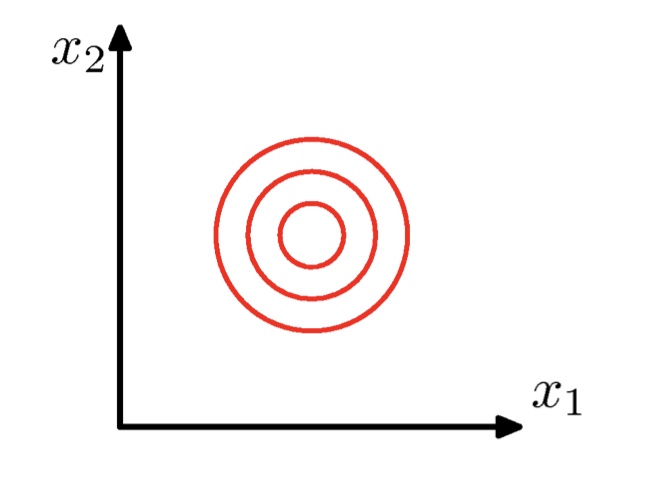
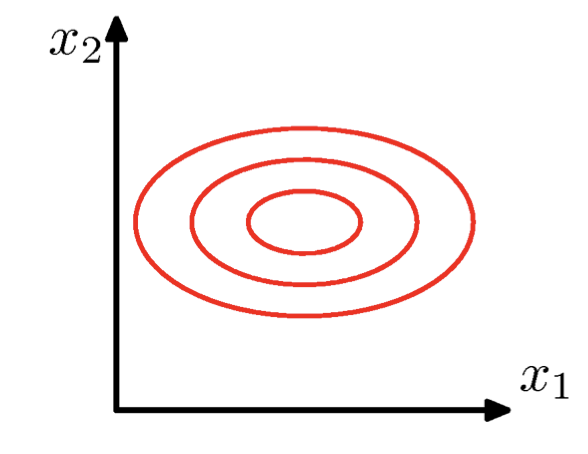
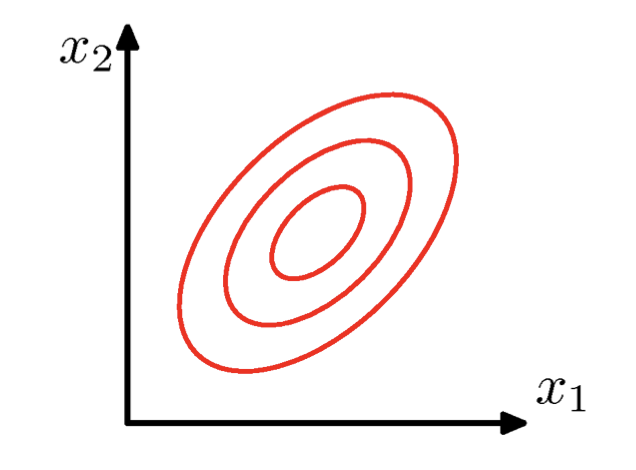
\(\Sigma\) = arbitrary (semidefinite) matrix:

• Specifies rotation (change of basis)
• Eigenvalues specify relative elongation


Mixture of Gaussians





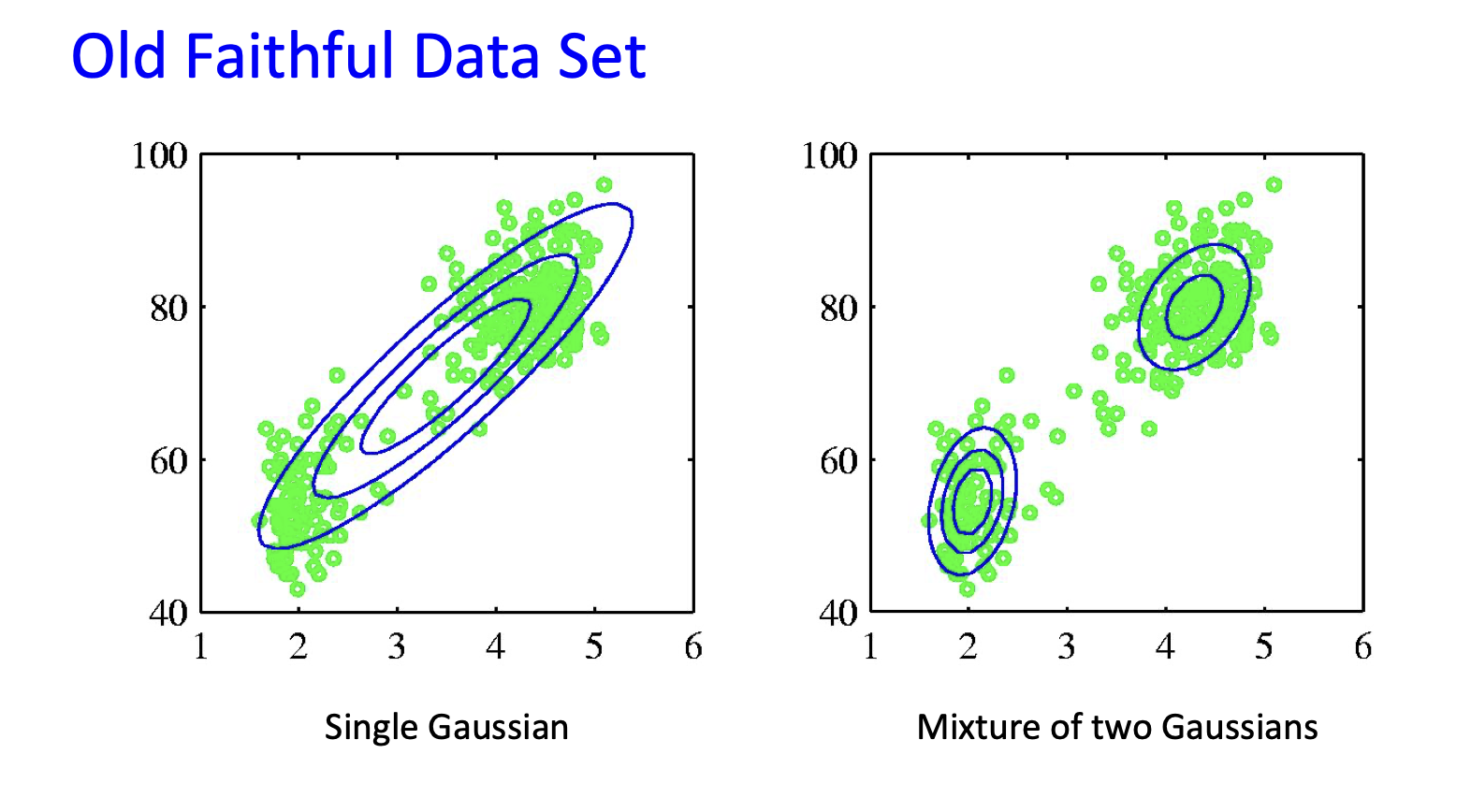
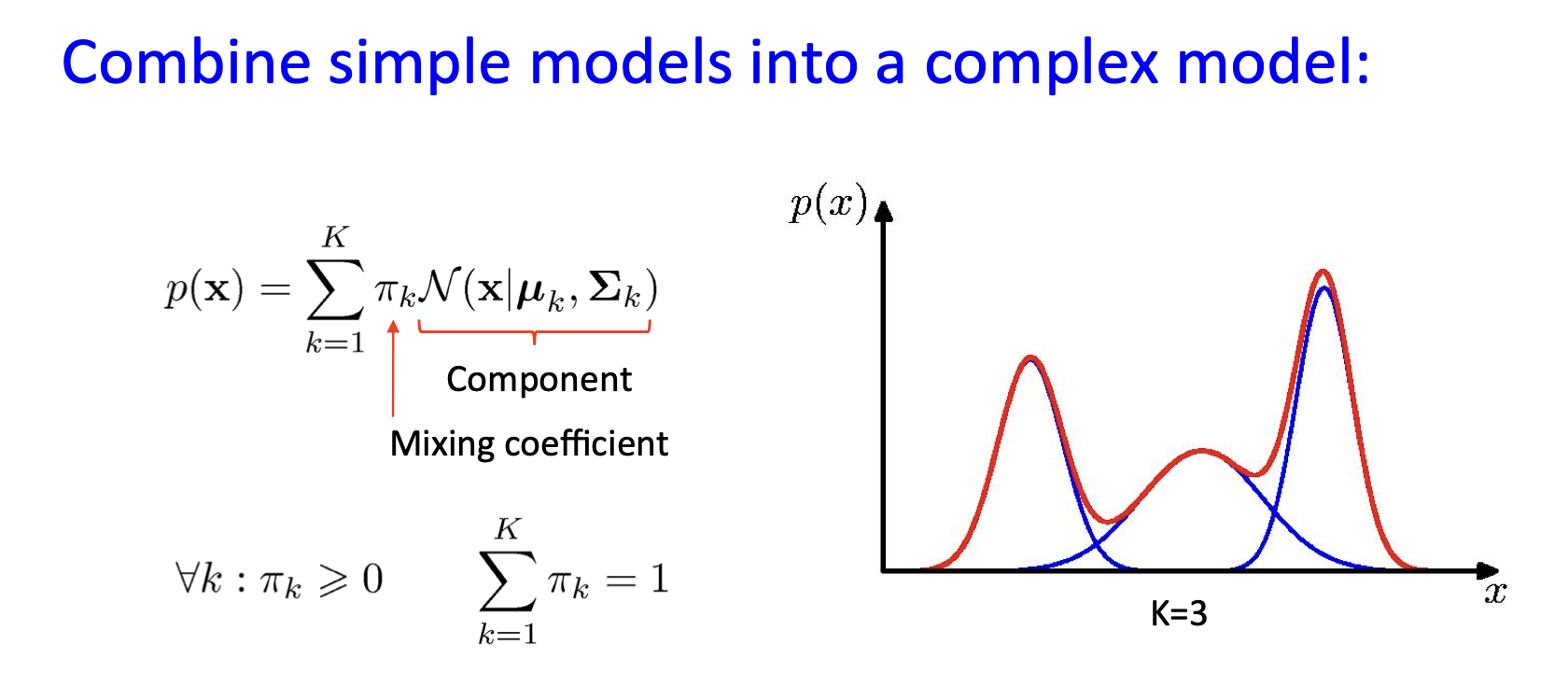
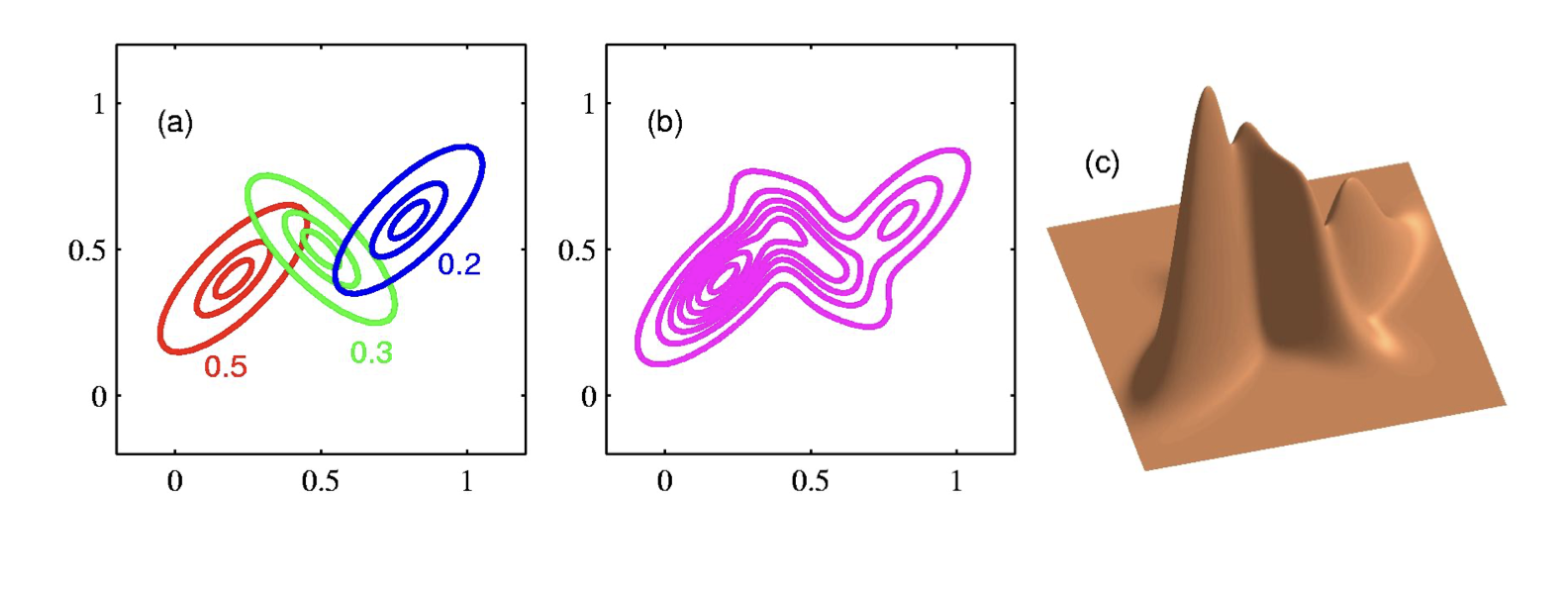
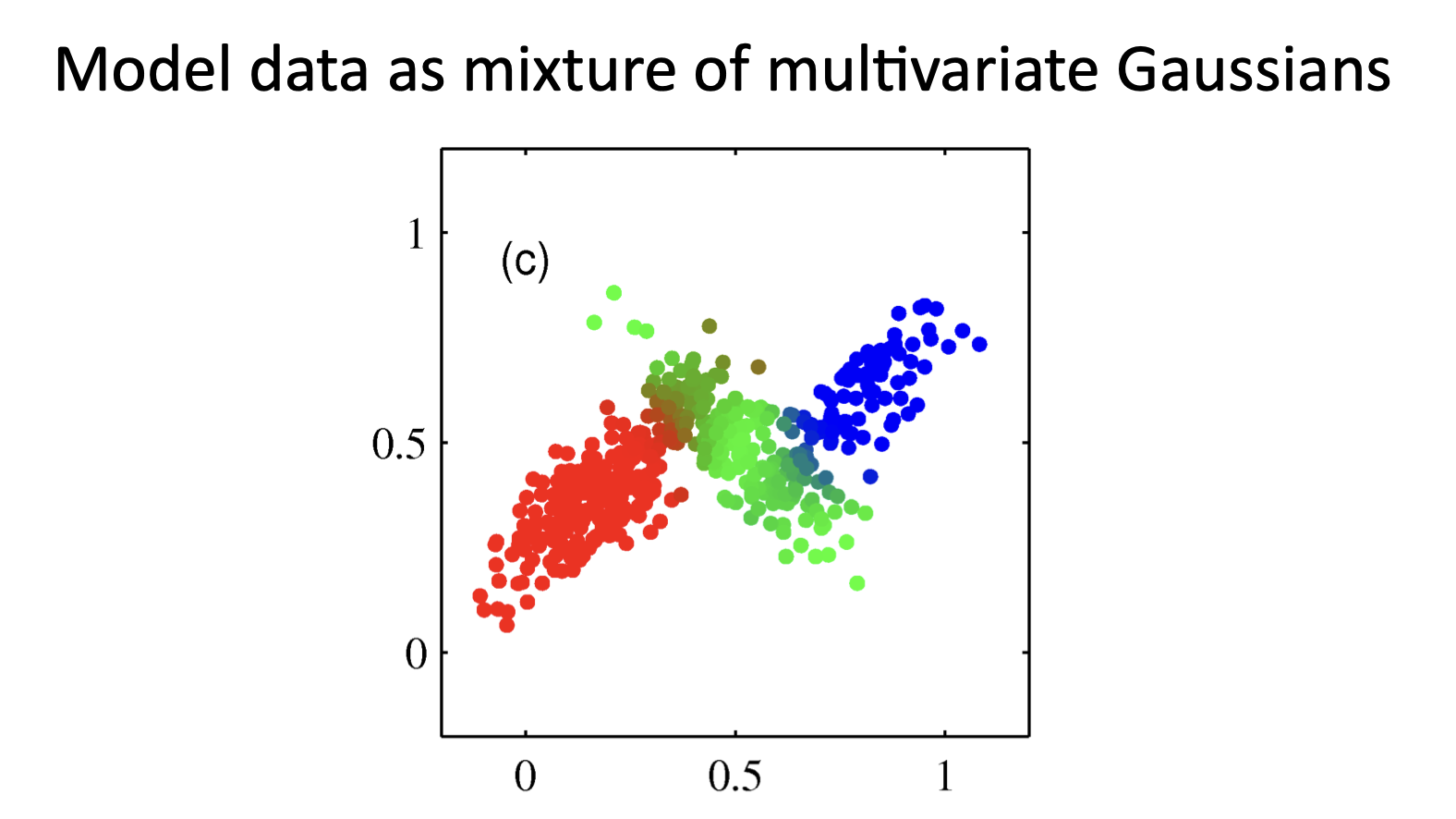
Shown is the posterior probability that a point was generated from the \(i^\text{th}\) Gaussian: \(\Pr(Y = i \mid x)\)

ML Estimation in Supervised Setting

• Univariate Gaussian

\[ \mu_{MLE} = \frac{1}{N} \sum_{i=1}^N x_i, \quad \sigma^2_{MLE} = \frac{1}{N} \sum_{i=1}^N (x_i - \hat{\mu})^2 \]

• Mixture of Multivariate Gaussians

  • ML estimate for each of the Multivariate Gaussians is given by, which just sums over \(x\) generated from the \(k^{th}\) Gaussian:
  \[ \mu^k_{ML} = \frac{1}{n} \sum_{j=1}^n x_j, \quad \Sigma^k_{ML} = \frac{1}{n} \sum_{j=1}^n (x_j - \mu^k_{ML})(x_j - \mu^k_{ML})^T \]

For unobserved data

• MLE:
  • \(\arg \max_\theta \prod_j P(y_j, x_j)\)
  • \(\theta\): all model parameters
    • e.g., class probabilities, means, and variances
• But we don't know \(y_j\)'s!
• Maximize marginal likelihood:
  • \(\arg \max_\theta \prod_j P(x_j) = \arg \max_\theta \prod_j \sum_{k=1}^K P(Y_j = k, x_j)\)
• Posterior Probability:

\[ P(y = k \mid x_j) \propto \frac{1}{(2\pi)^{m/2} \|\Sigma_k\|^{1/2}} \exp\left(-\frac{1}{2} (x_j - \mu_k)^T \Sigma_k^{-1} (x_j - \mu_k)\right) P(y = k) \]

• Marginal Likelihood:

\[ \begin{align*} \prod_{j=1}^m P(x_j) &= \prod_{j=1}^m \sum_{k=1}^K P(x_j, y = k)\\ & = \prod_{j=1}^m \sum_{k=1}^K \frac{1}{(2\pi)^{m/2} \|\Sigma_k\|^{1/2}} \exp\left(-\frac{1}{2} (x_j - \mu_k)^T \Sigma_k^{-1} (x_j - \mu_k)\right) P(y = k) \end{align*} \]

But usually no closed form solution, gradient is complex, lots of optimum. So we have the following which is a better way in the next section.

Expectation Maximization

• A clever method for maximizing marginal likelihood:
  • \(\arg \max_\theta \prod_j P(x_j) = \arg \max_\theta \prod_j \sum_{k=1}^K P(Y_j = k, x_j)\)
  • A type of gradient ascent that can be easy to implement (e.g., no line search, learning rates, etc.)
• Alternate between two steps:
  • Compute an expectation
  • Compute a maximization
• Not magic: still optimizing a non-convex function with lots of local optima
  • The computations are just easier (often, significantly so!)

EM: Two Easy Steps

• Objective:
  • \(\arg \max_\theta \log \prod_j \sum_{k=1}^K P(Y_j=k, x_j \mid \theta) = \sum_j \log \sum_{k=1}^K P(Y_j=k, x_j \mid \theta)\) (Notation is a bit inconsistent, parameters = \(\theta\) = \(\lambda\).
• Data:
  • \(\{x_j \mid j=1 \ldots n\}\)
• E-step: Compute expectations to "fill in" missing \(y\) values according to current parameters, \(\theta\)
  • For all examples \(j\) and values \(k\) for \(Y_j\), compute: \(P(Y_j=k \mid x_j, \theta)\)
• M-step: Re-estimate the parameters with "weighted" MLE estimates
  • \(\theta = \arg \max_\theta \sum_j \sum_k P(Y_j=k \mid x_j, \theta) \log P(Y_j=k, x_j \mid \theta)\)
• Note: Especially useful when the E and M steps have closed form solutions!


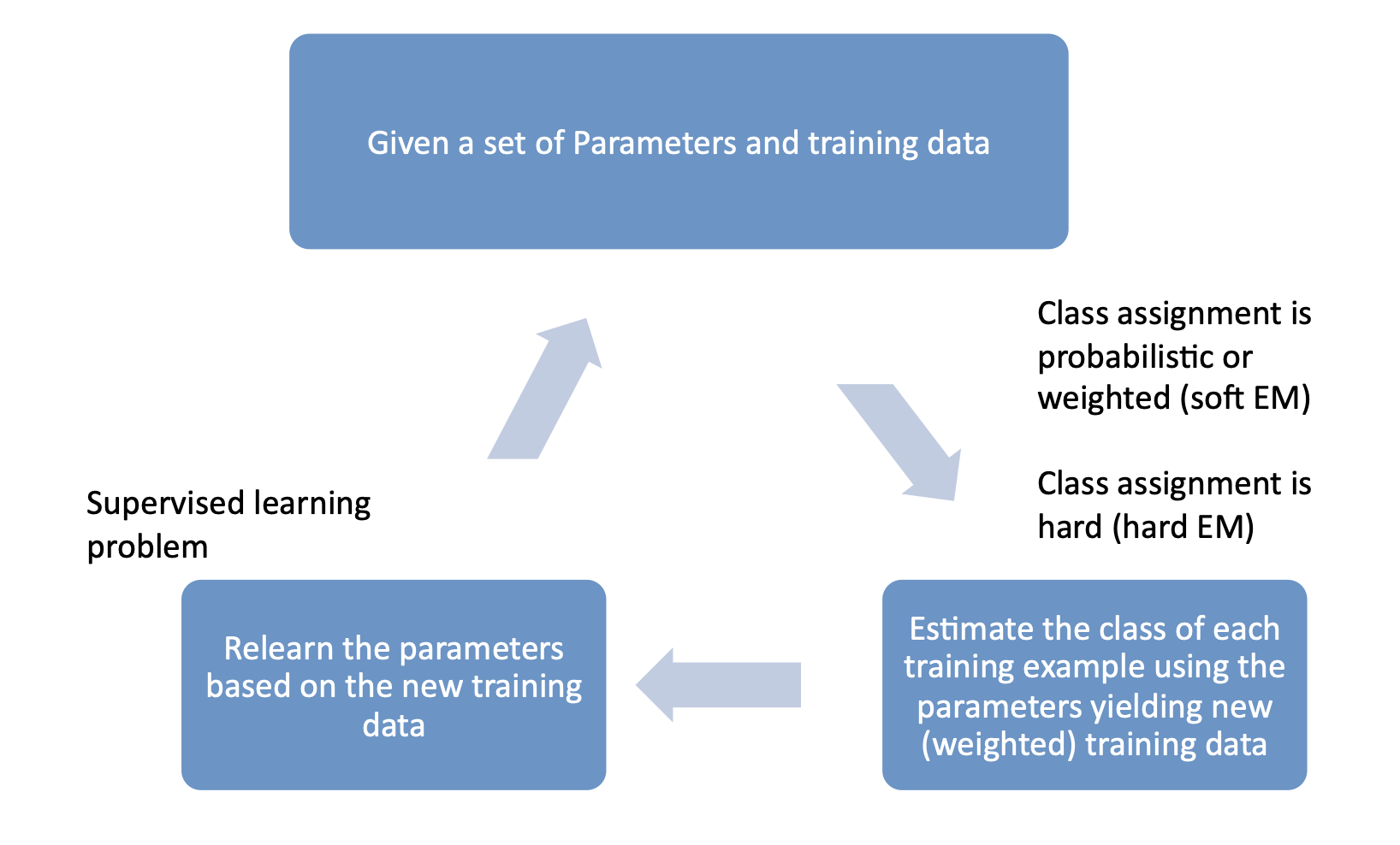
EM algorithm: Pictorial View

E.M. for General GMMs

• Iterate: On the \(t\)-th iteration let our estimates be \(\lambda_t = \{ \mu_1^{(t)}, \mu_2^{(t)}, \ldots, \mu_K^{(t)}, \Sigma_1^{(t)}, \Sigma_2^{(t)}, \ldots, \Sigma_K^{(t)}, p_1^{(t)}, p_2^{(t)}, \ldots, p_K^{(t)} \}\) where \(p_k^{(t)}\) is shorthand for estimate of \(P(y=k)\) on \(t\)-th iteration.
• E-step: Compute “expected” classes of all datapoints for each class \(P(Y_j = k \mid x_j, \lambda) \propto p_k^{(t)} \cdot p(x_j \mid \mu_k^{(t)}, \Sigma_k^{(t)})\) Just evaluate a Gaussian at \(x_j\).
• M-step: Compute weighted MLE for \(\mu\) given expected classes above where \(m\) is the number of training examples.

\[ \mu_k^{(t+1)} = \frac{\sum_j P(Y_j = k \mid x_j, \lambda) \cdot x_j}{\sum_j P(Y_j = k \mid x_j, \lambda)} \]

\[ \Sigma_k^{(t+1)} = \frac{\sum_j P(Y_j = k \mid x_j, \lambda) \cdot (x_j - \mu_k^{(t+1)})(x_j - \mu_k^{(t+1)})^T}{\sum_j P(Y_j = k \mid x_j, \lambda)} \]

\[ p_k^{(t+1)} = \frac{\sum_j P(Y_j = k \mid x_j, \lambda)}{m} \]

What if we do hard assignments?

• Iterate: On the \(t\)-th iteration let our estimates be \(\lambda_t = \{ \mu_1^{(t)}, \mu_2^{(t)}, \ldots, \mu_K^{(t)} \}\)
• E-step: Compute "expected" classes of all datapoints \(P(Y_j = k \mid x_j, \mu_1, \ldots, \mu_K) \propto \exp\left(-\frac{1}{2\sigma^2} \|x_j - \mu_k\|^2\right)\cancel{P(Y_j=k)}\) (Here, the term \(P(Y_j = k)\) is omitted due to hard assignments represented by \(\delta\), which indicates hard assignment to the "most likely" or nearest cluster.)
• M-step: Compute most likely new \(\mu\) given class expectations where \(\delta(Y_j = k, x_j)\) represents hard assignment to cluster \(k\) for datapoint \(x_j\).

\[ \cancel{\mu_k = \frac{\sum_{j=1}^m P(Y_j = k | x_j) \cdot x_j}{\sum_{j=1}^m P(Y_j = k| x_j)}} \]

\[ \mu_k = \frac{\sum_{j=1}^m\delta(Y_j = k, x_j) \cdot x_j}{\sum_{j=1}^m \delta(Y_j = k, x_j)} \]

Equivalent to k-means clustering algorithm!

Note

❗

ChatGPT said:

In the context of clustering algorithms, such as the Expectation-Maximization (EM) algorithm adapted for k-means, "hard assignment" refers to the practice of assigning each data point to exactly one cluster without ambiguity or uncertainty. Here's what this means more specifically:

1. Hard vs. Soft Assignment:
   • Soft Assignment (typical in EM with Gaussian Mixture Models): Each data point is assigned a probability of belonging to each cluster, representing its likelihood of membership in every cluster. This is based on the Gaussian probability density, where the mean and covariance of each cluster influence how likely a data point is to belong to that cluster. Soft assignments allow a data point to be fractionally part of multiple clusters simultaneously.
   • Hard Assignment (used in k-means and adapted EM): Each data point is assigned to the single cluster to which it is most similar, usually based on Euclidean distance to the cluster centers. Each point is definitively categorized into only one cluster, making this approach simpler and often faster but potentially less nuanced.
2. Implementation in the EM Algorithm:
   • E-step (Expectation step): In standard EM, this step would calculate the expected value of the assignment variables (e.g., probabilities for Gaussian mixtures). For hard assignments, this step simplifies into choosing the nearest cluster center for each data point, similar to the assignment step in k-means. Mathematically, it's often indicated with a Kronecker delta function, \(\delta\), which equals 1 if the condition is true (the chosen cluster is the nearest) and 0 otherwise.
   • M-step (Maximization step): The parameters (in this case, just the means or centroids of the clusters) are recalculated based solely on the data points assigned to each cluster. Variance is typically not considered in the hard assignment scenario since the focus is on centroids, akin to k-means.
3. Implications:
   • Simplicity: Hard assignments simplify the computation as each data point affects only one cluster's calculation during the M-step.
   • Loss of Information: Potential information from data points that might have significant probabilities of belonging to multiple clusters is lost since each point can only contribute to the cluster to which it has been assigned.
   • Effectiveness: For well-separated data, hard assignments might perform robustly and efficiently, making them ideal for certain applications where the true clusters are distinct and non-overlapping.

The general learning problem with missing data

• Marginal Likelihood: \(X\) is observed, \(Z\) (e.g. the class labels \(Y\)) is missing:

\[ \begin{align*} \ell(\theta : D) &= \log \prod_{j=1}^m P(x_j \mid \theta) \\ &= \sum_{j=1}^m \log P(x_j \mid \theta) \\ &= \sum_{j=1}^m \log \sum_Z P(x_j, z \mid \theta) \end{align*} \]

• Objective: Find

\[ \arg \max_{\theta} \ell(\theta : \text{Data}) \]

E-step

• X is observed, Z is missing

• Compute probability of missing values given current choice of \(\theta\):

  • \(Q(z \mid x_j)\) for each \(x_j\)
    • e.g., probability computed during classification step
    • corresponds to "classification step" in K-means
  \[ Q^{(t+1)}(z \mid x_j) = P(z \mid x_j; \theta^{(t)}) \]

Properties of EM

• We will prove that:
  • EM converges to a local minima.
  • Each iteration improves the log-likelihood.
• How? (Same as k-means)
  • E-step can never decrease likelihood.
  • M-step can never decrease likelihood.

Jensen's Inequality

• Theorem:

\[ \log \sum_Z P(z) f(z) \geq \sum_Z P(z) \log f(z) \]

Applying Jensen's Inequality

• Use:

\[ \log \sum_Z P(z) f(z) \geq \sum_Z P(z) \log f(z) \]

• For the EM algorithm:

\[ \begin{align*} \ell(\theta^{(t)} \cdot D) &= \sum_{j=1}^m \log \sum_Z Q^{(t+1)}(z \mid x_j) \frac{P(z, x_j \mid \theta^{(t)})}{Q^{(t+1)}(z \mid x_j)} \\ &\geq \sum_{j=1}^m \sum_Z Q^{(t+1)}(z \mid x_j) \log \left(\frac{P(z, x_j \mid \theta^{(t)})}{Q^{(t+1)}(z \mid x_j)}\right) \\ &= \sum_{j=1}^m \sum_Z Q^{(t+1)}(z \mid x_j) \log \left(P(z, x_j \mid \theta^{(t)})\right) - \sum_{j=1}^m \sum_Z Q^{(t+1)}(z \mid x_j) \log \left(Q^{(t+1)}(z \mid x_j)\right) \end{align*} \]

• This results in:

\[ \ell(\theta^{(t)} \cdot D) \geq \sum_{j=1}^m \sum_Z Q^{(t+1)}(z \mid x_j) \log P(z, x_j \mid \theta^{(t)}) + \sum_{j=1}^m H(Q^{(t+1), j}) \]

where \(H(Q^{(t+1), j})\) represents the entropy of the distribution \(Q^{(t+1)}\) for each observation \(j\).

The M-step

• Lower bound:

\[ \ell(\theta^{(t)} \cdot D) \geq \sum_{j=1}^m \sum_Z Q^{(t+1)}(z \mid x_j) \log P(z, x_j \mid \theta^{(t)}) + \sum_{j=1}^m H(Q^{(t+1)}, j) \]

(The last term is a constant with respect to \(\theta\))

• Maximization step:

  \[ \theta^{(t+1)} \leftarrow \arg \max_{\theta} \sum_{j=1}^m \sum_Z Q^{(t+1)}(z \mid x_j) \log P(z, x_j \mid \theta) \]
  • We are optimizing a lower bound!

What you should know

• Mixture of Gaussians
  • Coordinate ascent, just like k-means.
  • How to “learn” maximum likelihood parameters (locally max. like.) in the case of unlabeled data.
  • Relation to K-means:
    • Hard/soft clustering.
    • Probabilistic model.
• Remember, EM for mixture of Gaussians:
  • EM can get stuck in local minima,
  • And empirically it DOES.